
I recently started experimenting with Nanodots Magnetic Constructors (a 216 magnet set of remarkably strong (and fun!) little spherical (NdFeB) magnets. They are enjoyable to play with just from a tactile, sensory perspective, since they are like a set of high-tech micro-planets you can squeeze and morph in your hand like modeling clay … and the next moment, when you pull the amorphous mass apart, you get dynamic strings of metallic pearls that have amazing tenacity to maintain the connection to the whole. I’m just getting started in using Nanodots to explore my primary interest in geometric shapes.
Here are a few photos of Nanodots in 2D (flat shapes in a plane).


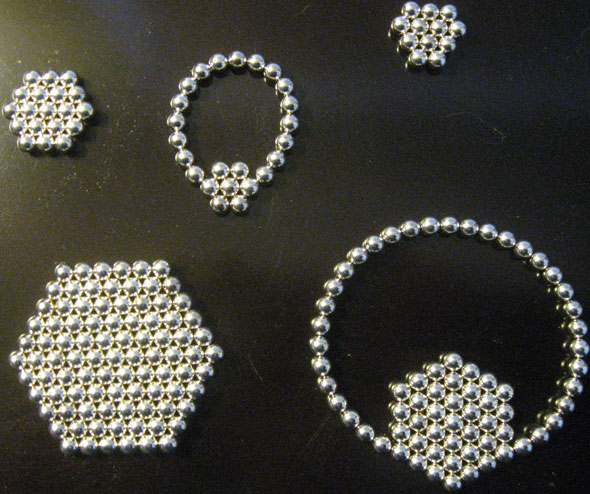
As you might imagine, if you make two shapes and put them close together on a flat surface, suddenly you find yourself with one shape! Symbolically, the magnetic principle abhors duality! 🙂 When you have smallish shapes in close proximity, but not so close that they join, you can rotate one and the neighboring shapes will rotate in tandem, almost like invisible gears; cool! 🙂
I’ve made a few simple 3D geometries with Nanodots, but will need to spend more time and try a variety of polyhedra and other shapes. Interestingly, a few of the shapes (like the tetrahedron which moves immediately into a square and the octahedron which jumps into a more space-filling arrangement) are a bit tricky to hold (without some external constraint), since their geometries when made of magnetic spheres tend to fly apart and rearrange into more stable magnetic alliances. I think I see why the seasoned users make stable clusters and then make the larger shapes out of these smaller clusters.
Since their magnetic properties lend toward modeling with larger clusters that aren’t as influenced by smaller numbers of spheres, I’ll explore further with larger sets. Here are some excellent examples that others (mostly with larger sets than 216) have made.
Squishy Icosahedron Frame – YouTube
There are LOTS of great examples (both videos and static images) of polyhedra and other geometric shapes that are superb uses of Nanodots here; enjoy!