Geometry Code

Sacred Geometry Media Resource Blog

Sacred Geometry Resources, Books, Conversations, Art Prints, Cards, Screensavers, Videos, Patterns, Blog and more
You are here: Home / Archives for 3D Geometries

3D Geometries

Encyclopedia of Polyhedra By George W. Hart … and other geometric gems

by

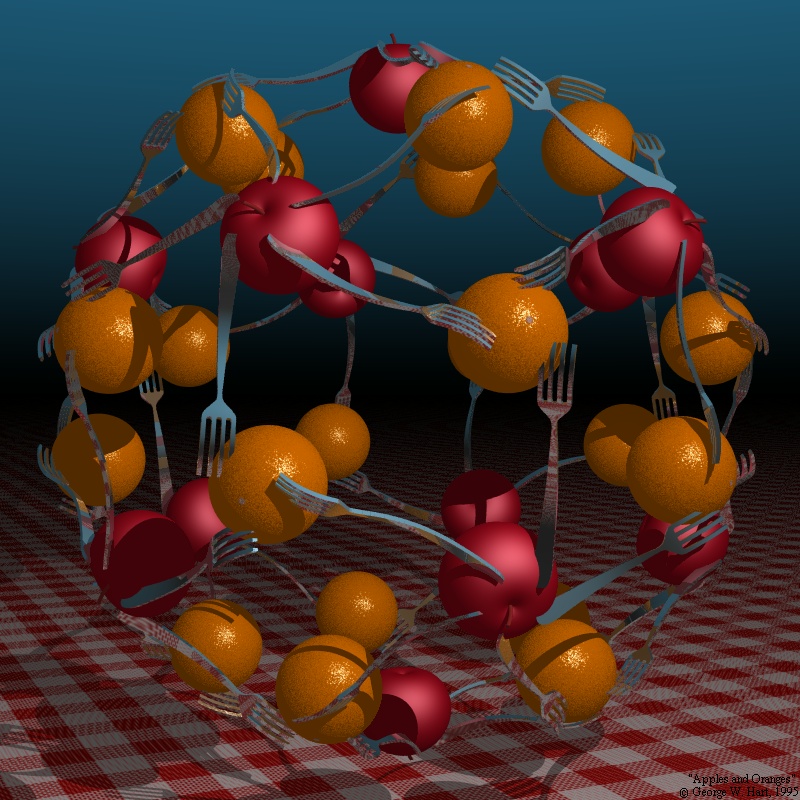
Apples and Oranges by George W. Hart https://www.georgehart.com/Applorng.html
Apples and Oranges by George W. Hart
https://www.georgehart.com/Applorng.html

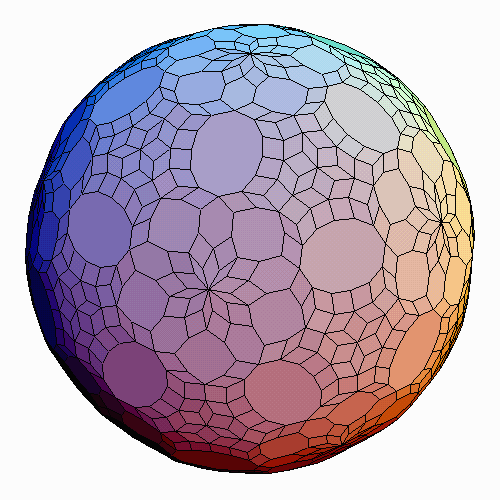
It’s time to revisit the work of other polyhedra enthusiasts. Of particular note (having crossed my digital path again recently) is George W. Hart who has shared some excellent resources along these lines (faces, vertices, etc.) for decades. Here’s one gold mine to explore: Virtual Polyhedra: The Encyclopedia of Polyhedra By George W. Hart. Here is part of the table of contents and highly recommended if you want to explore the genres and categories of polyhedra; lots of great imagery, rotatable 3D models (rotate them with your mouse), facts and details:

Perhaps the most well-known and ubiquitous polyhedral shapes have fold-up models (and related patterns) for the first 3 categories above in Sacred Geometry Design Sourcebook (SGDS pages 196-220) and also on this website for the 5 Platonic Solids and 13 Archimedean Solids as well as Illustrations of Platonic And Archimedean Solids, Math Tables for Platonic And Archimedean Solids (and much more about polyhedra on this website.

compound of five cubes by George W. Hart
compound of five cubes by George W. Hart

If you exhaust this generous resource (or somehow overlook a few gems) here are more of his contributions – the videos are particularly helpful if you want to replicate his constructions:

Stained Glass Ball By George W. Hart https://www.georgehart.com/stained_glass.html
Stained Glass Ball By George W. Hart
https://www.georgehart.com/stained_glass.html

Non-Euclidean Geometries

by

At the end of last month’s post we gave this example of non-Euclidean geometric art inspired by M. C. Escher’s pioneering graphics which explored various geometries and illusory perspectives.

Also noted in last month’s post, here’s a still image related to a scene in the movie “Inception” that had a physical implementation of an impossible (never-ending) staircase; our limited geometric perspectives can deceive us:

Penrose stairs in the movie "Inception"

Since there’s no point in “reinventing the wheel” I’ll quote from Wikipedia’s definition for non-Euclidean geometry, also since I’m a novice in that field, but an admirer of art and imagery inspired by that geometry that stretches our imaginations:

In mathematics, non-Euclidean geometry consists of two geometries based on axioms closely related to those that specify Euclidean geometry. As Euclidean geometry lies at the intersection of metric geometry and affine geometry, non-Euclidean geometry arises by either replacing the parallel postulate with an alternative, or relaxing the metric requirement. In the former case, one obtains hyperbolic geometry and elliptic geometry, the traditional non-Euclidean geometries. When the metric requirement is relaxed, then there are affine planes associated with the planar algebras, which give rise to kinematic geometries that have also been called non-Euclidean geometry.

The principles below (from the next section in the Wikipedia page) reveal how the behavior of parallel and perpendicular lines differs in two common non-Euclidean realms; Hyperbolic Geometry and Elliptic Geometry: with a graphic demonstrating how if we don’t make certain Euclidean assumptions about space (e.g. parallel and perpendicular line behavior) such as the requirement that the sum of the angles of a triangle add up to 180°.

The essential difference between the metric geometries is the nature of parallel lines. Euclid‘s fifth postulate, the parallel postulate, is equivalent to Playfair’s postulate, which states that, within a two-dimensional plane, for any given line l and a point A, which is not on l, there is exactly one line through A that does not intersect l. In hyperbolic geometry, by contrast, there are infinitely many lines through A not intersecting l, while in elliptic geometry, any line through A intersects l.

Another way to describe the differences between these geometries is to consider two straight lines indefinitely extended in a two-dimensional plane that are both perpendicular to a third line (in the same plane):

  • In Euclidean geometry, the lines remain at a constant distance from each other (meaning that a line drawn perpendicular to one line at any point will intersect the other line and the length of the line segment joining the points of intersection remains constant) and are known as parallels.

  • In hyperbolic geometry, they diverge from each other, increasing in distance as one moves further from the points of intersection with the common perpendicular; these lines are often called ultraparallels.

  • In elliptic geometry, the lines converge toward each other and intersect.

Here’s a simple graphic that gives a hint about the fundamentals of these mind-warping geometries that might be akin to warm-up exercises for four-dimensional (and beyond) geometries and polytopes, which we like to explore on this website now and then.

Comparison of geometries: Elliptic, Euclidean, Hyperbolic
By Cmglee – Own work, CC BY-SA 4.0, Link

By Cmglee – Own work, CC BY-SA 4.0, Link

Here’s an example of hyperbolic geometric art:

Rhombitriheptagonal tiling
Rhombitriheptagonal tiling – Parcly Taxel, Public domain, via Wikimedia Commons

Here’s an astronaut’s perspective example of how the sum of the angles of a non-Euclidean triangle can add up to more than 180° on the surface of a spheroid (our beloved planet):

Spherical geometry example: sum of angles exceeds 180 degrees
Spherical geometry example: sum of angles exceeds 180 degrees; Lars H. Rohwedder, Sarregouset https://en.wikipedia.org/wiki/File:Triangles_(spherical_geometry).jpg

For further exploration and many more wonderful and artistic images, I recommend this article “The Use of Non-Euclidean Geometry in Art” on the naiadseye blog …
and this post “Non-Euclidean Geometry Art August 4, 2014″ on “Harrison Hartle’s Art/Music/Theater F200 blog.”

The latter has this excellent TED talk video about “The beautiful math of coral” by Margaret Wertheim (2009); I first learned of this fascinating realm of modeling coral reefs (and many other “hyperbolic geometry” life forms with crochet hooks) from my colleague Libby M. in Oregon at a Geometers meeting about 20 years ago who had made and shared several knitted models inspired by this work:

Margaret Wertheim (in the video above) references the work of Froebel, an educational pioneer featured on this website. Froebel-inspired products are available from RedHen Books and Toys featuring unique, hard-to-find educational materials, toys and books such as Bradford Hansen-Smith’s circle folding videos, books and supplies.

In addition to the other affiliates on the GeometryCode.com website featured in the sidebar on every page that help support this “labor of love” website, please check out Ka Gold Sacred geometry jewelry by artist David Weitzman including wearable geometric art including Flower of Life, Seed of Life, Golden Spiral, Fruit of Life, Vesica Piscis, Star tetrahedron “Merkaba”, Fibonacci Whirling Squares Spiral “Phi”, Metatron’s Cube, Chambered Nautilus, Labyrinth, Torus Tube, Tetractys, Sri Yantra mandala, Tree of Life, and Hexagram (Star of David).

The Wolfram MathWorld page on Non-Euclidean Geometry also has many pertinent links and resources.

The Bridges organization has more related material on the subject of mathematical art.

In case you still need a 2025 calendar, there are 10 months left in the year as of the date of this post, and 2025 calendars are still available – as well as my over-quarter-century-old timeless classic reference book, Sacred Geometry Design Sourcebook – Universal Dimensional Patterns, heavily inspired by Escher, and other geometric luminaries.

M. C. Escher’s Geometry and Illusory Perspectives Revisited

by

Musing about how the interpretations of our physical senses are often misled by optical (and other) illusions, I was reflecting on being inspired decades ago by the classic M. C. Escher images in the book (The Graphic Work of M.C. Escher Introduced and Explained By the Artist Paperback – January 1, 1973
by M. C. Escher). The cover of this Escher book features an image of a small-stellated dodecahedron with cutouts in half of the lower portion of each triangular face of each stellating pentagonal pyramid permitting polychromatic reptile heads and limbs to protrude (Gravity, June 1952. Lithograph and Watercolour.) Many of Escher’s illustrations demonstrate these sensory deceptions – which can be beneficially used to inspire a willingness to see things from multiple (open-minded) perspectives –  such as images in his Impossible Constructions and Mathematical galleries and other classic images employing space-filling tessellation patterns and numerous instances of multiple simultaneous perspectives. In addition to an early introduction to Platonic Solids, Archimedean Solids, stellations, and more in the polyhedral realms, Escher’s pioneering visionary art seemed to suggest to me the value of exploring perspectives beyond  what our unreliable senses (and our misinterpreting minds) report and stoked a curiosity to explore realms beyond ordinary viewpoints. My other primary blog is devoted to these metaphysical explorations.

Examples which show the distortions of our sensory misinterpretations include these images (I haven’t copied the images due to copyright requirements, so please tap the links on this post to check out these example Escher gems (many more in these extensive archives: Selected Works by M.C. Escher):

Here is a close-up of Escher-inspired tiles that adorn the front yards of at least two local homes in Green Valley, AZ; photographed on nearby neighborhood walks during the past 18 months.

interlocking Escher-inspired reptile tiles

For further exploration, check out:

The end of the last article above reminded me that there’s a scene in the movie “Inception” (a fave flick) that had a physical implementation of one of these impossible (never-ending) staircases. featured in popular Escher image:

Escher’s art also explored Non-Euclidean Geometries, which will be featuring in next month’s post. The art below reflects an example of an Escher-inspired Non-Euclidean geometry.

In case you still need a 2025 calendar, there are 11 months left in the year as of the date of this post, and 2025 calendars are still available – as well as my over-quarter-century-old timeless classic reference book, Sacred Geometry Design Sourcebook – Universal Dimensional Patterns, heavily inspired by Escher, and other geometric luminaries.

Geometric gemstones

by

triangular geometric gemstone: Hashnu trioptic blastRecently a friend (Rick Fuller) showed me his gemstone grinding equipment including two grinders; one with a caliper-style readout to set grinding angles and another with a digital readout. My experience in this area is negligible, but the designs of cut gemstones seem profoundly connected to 3-dimensional solid geometry and all the laws, theorems, and insights gleaned over centuries about geometric proportions and more. Geometry is everywhere, and the geometric (polygonal) facets of countless gemstones are an excellent example.

Thinking about both the microscopic and macroscopic geometries involved and how this might be optimized in this endeavor, I did a quick online search for “gemstones cut to angles that match atomic lattice structure” and found this interesting AI-generated response:

Gemstones and Lattice Structure

Based on the search results, Corundum (Al2O3) is a crystalline mineral that exhibits a hexagonal crystal system. Its lattice parameters are well-defined, and the angles between its crystal axes are fixed at 90° and 120°.

In the context of gemstone cutting, Corundum is notable for its unique properties. Rubies and sapphires, which are varieties of Corundum, can be cut to specific angles to enhance their optical properties and brilliance. The cutting angles are designed to match the atomic lattice structure of the mineral, taking into account the hexagonal symmetry of the crystal.

For example, the refractive indices and birefringence of Corundum can be optimized by cutting the gemstone at specific angles, such as:

  • The “ideal cut” for rubies and sapphires, which involves cutting the stone with a pavilion angle of around 40-41° and a crown angle of around 25-30°. This angle combination minimizes internal reflections and maximizes brilliance.
  • The “step-cut” or “tabby cut,” which involves cutting the stone with a series of flat, parallel surfaces. This cut style is often used for sapphires and takes advantage of Corundum’s hexagonal symmetry to reduce birefringence and improve color distribution.

While other gemstones may not have the same level of precision in their cutting angles, Corundum’s unique properties make it an ideal candidate for cutting to angles that match its atomic lattice structure. This attention to detail can result in more vibrant colors, higher brilliance, and a more pleasing visual appearance.

Searching for related topics led to these quasi-random resources:

… and since we’re on the topic of geometric jewelry, check out Sacred geometry jewelry by artist David Weitzman (Ka-Gold) … Related Content: Flower of Life, Seed of Life, Golden Spiral, Fruit of Life, Vesica Piscis, Star tetrahedron “Merkaba”, Fibonacci Whirling Squares Spiral “Phi”, Metatron’s Cube, Chambered Nautilus, Labyrinth, Torus Tube, Tetractys, Sri Yantra mandala, Tree of Life, Hexagram (Star of David).

pentagonal geometric gemstone

Sacred Geometry in the documentary “Leonardo da Vinci” by Ken Burns

by

Leonardo da Vinci (Ken Burns PBS documentary) screen snap of geometric shadow illustration

This evening we finished watching the excellent 2-part documentary “Leonardo da Vinci” by Ken Burns (and others) which – like everything Ken touches – was wonderful. No surprise, and, of course, highly recommended. Please support PBS and your favorite public/community/independent media, too!

Initially, I thought I would use my default browser (Brave) to find some still images from the documentary, and using this search term: “sacred geometry in Ken Burns Leonardo documentary” got this interesting – not bad! – AI-generated response:

In the Ken Burns documentary about Leonardo da Vinci, sacred geometry is explored as a key aspect of da Vinci’s work and thought process. Da Vinci’s use of geometric shapes and proportions in his art and designs is highlighted as a way to understand the underlying structure of the universe.

  • Geometric Lines and Proportions: The documentary shows how da Vinci used geometric lines and proportions in his paintings, such as the Mona Lisa and The Last Supper, to create a sense of balance and harmony. These geometric elements are also seen in his designs for machines and buildings.
  • The Vitruvian Man: Da Vinci’s famous drawing, the Vitruvian Man, is featured in the documentary as an example of his use of sacred geometry. The drawing depicts a nude male figure inscribed within a circle and square, demonstrating the mathematical proportions of the human body.
  • Nature and Geometry: The documentary explores how da Vinci saw geometry as a way to understand the natural world. He believed that the patterns and shapes found in nature, such as the spiral of a shell or the branching of trees, were evidence of a deeper geometric order.
  • Da Vinci’s Notebooks: The documentary features da Vinci’s notebooks, which contain his thoughts on geometry, proportion, and the natural world. These notebooks show how da Vinci saw geometry as a way to understand the underlying structure of the universe.

Overall, the documentary presents sacred geometry as a central aspect of da Vinci’s work and thought process, and shows how it influenced his art, designs, and understanding of the natural world.

Check it out. The topic of sacred geometry – although not referred to by that name – makes a cameo appearance in this 2-part series among Leonardo’s wide range of mathematical and scientific interests which, in turn, are just a small portion of the depth and breadth of the realms explored by this amazing historical figure. I appreciated how this “Renaissance” icon appeared to embrace anything and everything as a classroom for for generalizing a deeper understanding, as Egyptologist John Anthony West told us was the goal in ancient Egypt, rather than encouraging specialization.

(The image at the top of this post is a screen snap from the documentary. There are way too many amazing illustrations, so this is just one of the numerous featured in this program.)

In addition to the Vitruvian Man, this PBS program also showed a generous assortment of da Vinci’s geometric and geometrically-oriented mechanical drawings of both natural and man-made objects.

When I was putting together my first book, I was inspired by the geometry of one of da Vinci’s sketches of an “ideal church” and made this (Claris CAD) image from that concept (page 191 from Sacred Geometry Design Sourcebook):

Sacred Geometry Design Sourcebook (page191) - Ideal Church (adapted from a sketch by Leonardo da Vinci)

Some of the less obvious geometries in the “Vitruvian Man” (a.k.a. “Measure of Man”) by da Vinci – in addition to the more widely known phi proportion: toes-to-navel and navel to top of head – are revealed on page 190 of the SGDS book:

Sacred Geometry Design Sourcebook (page 190) Leonardo da Vinci: Vitruvian Man (Measure of Man) illustration showing sacred geometry proportions

Enjoy!